DSLR-Sensor justieren nach einer Astro-Modifikation
Die übliche Methode, einen ausgebauten, federgelagerten Sensor nach dem Wiedereinbau in die Kamera zu justieren, besteht ja darin, die originale Position der Schrauben zu markieren und die Umdrehungen bis zum Anschlag zu zählen. Das ist nicht sehr genau und kann auch schiefgehen, wenn beim Markieren der Positionen oder Zählen der Umdrehungen ein Fehler passiert.
Die einzige andere Methode, auf die ich gestoßen bin, beruht auf einer mechanischen Präzisionsmessung, die ich aber mit meinen Mitteln nicht durchführen kann.
Deshalb habe ich mir etwas überlegt, das einfacher zu machen ist. Man braucht dazu einen Laserpointer, ein Stückchen Glas und – das ist das Komplizierteste – einen halbwegs stabilen Aufbau dazu.
Meine Methode vergleicht die Reflexionen eines Laserstrahls am Sensor und an einem Glasscheibchen, das auf dem Bajonett der Kamera aufgelegt wird.
Der erste Teil der Justage besteht dann darin, die Verkippung des Sensors so einzustellen, dass die beiden reflektierten Strahlen möglichst exakt zusammenfallen. Dabei kann man dann sogar überprüfen, ob ein in der Kamera verbleibendes LPF1-Filter korrekt sitzt, denn das produziert einen eigenen Reflex, der die anderen möglichst treffen sollte.
Im einfachsten Fall lässt man die reflektierten Strahlen auf eine weit entfernte Wand fallen und prüft, wie weit die Reflexe auseinander liegen. Praktischer ist ein kleiner Schirm mit einem Loch im Zentrum, durch das der Laserstrahl auf den Sensor trifft, wie hier skizziert:
Die einzige andere Methode, auf die ich gestoßen bin, beruht auf einer mechanischen Präzisionsmessung, die ich aber mit meinen Mitteln nicht durchführen kann.
Deshalb habe ich mir etwas überlegt, das einfacher zu machen ist. Man braucht dazu einen Laserpointer, ein Stückchen Glas und – das ist das Komplizierteste – einen halbwegs stabilen Aufbau dazu.
Meine Methode vergleicht die Reflexionen eines Laserstrahls am Sensor und an einem Glasscheibchen, das auf dem Bajonett der Kamera aufgelegt wird.
Der erste Teil der Justage besteht dann darin, die Verkippung des Sensors so einzustellen, dass die beiden reflektierten Strahlen möglichst exakt zusammenfallen. Dabei kann man dann sogar überprüfen, ob ein in der Kamera verbleibendes LPF1-Filter korrekt sitzt, denn das produziert einen eigenen Reflex, der die anderen möglichst treffen sollte.
Im einfachsten Fall lässt man die reflektierten Strahlen auf eine weit entfernte Wand fallen und prüft, wie weit die Reflexe auseinander liegen. Praktischer ist ein kleiner Schirm mit einem Loch im Zentrum, durch das der Laserstrahl auf den Sensor trifft, wie hier skizziert:
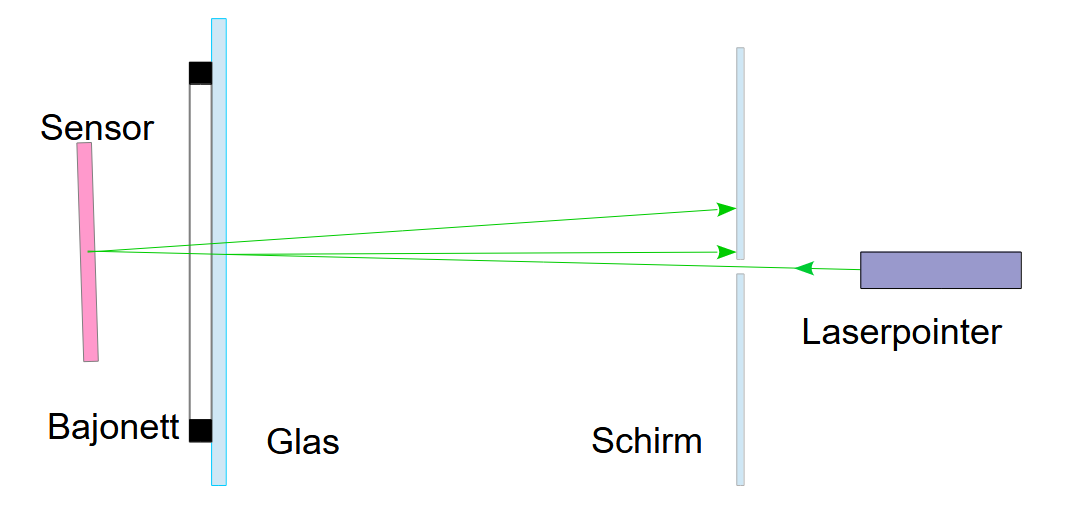
Hier sind nur die wichtigsten Reflexe skizziert. Tatsächlich bekommt man vom Glas je einen Reflex von der Vorder- und der Rückseite, die aber bei senkrechter Einstrahlung zusammenfallen. Dasselbe gilt für die LFP1 und LPF2 Filter. Vom Sensor kommen zwei Reflexe vom Deckglas und einer von seiner Oberfläche.
Eine Warnung noch zum Laser-Pointer: Die Exemplare, die es sehr günstig direkt in China zu kaufen gibt, funktionieren meiner Erfahrung nach gut, aber sie bringen zum Teil deutlich mehr Leistung, als gut für unsere Augen ist. Vorsicht im Umgang mit solchen Teilen ist also durchaus angeraten!
Winkeljustage
Das ist ein Reflex-Bild von einer unmodifizierten Kamera im Projektionsabstand von etwa vier Metern:
Eine Warnung noch zum Laser-Pointer: Die Exemplare, die es sehr günstig direkt in China zu kaufen gibt, funktionieren meiner Erfahrung nach gut, aber sie bringen zum Teil deutlich mehr Leistung, als gut für unsere Augen ist. Vorsicht im Umgang mit solchen Teilen ist also durchaus angeraten!
Winkeljustage
Das ist ein Reflex-Bild von einer unmodifizierten Kamera im Projektionsabstand von etwa vier Metern:
Der hellste Punkt links oben stammt vom Glas auf dem Bajonett, der untere vom Sensor, der dritthellste von den Filtern. Man sieht, dass die Werksjustierung auch nicht ganz perfekt ist, zumindest bei Kameras, die schon länger in Gebrauch sind. (Wer die Verkippung mal ausrechnen mag: Das Raster im Bild ist 5 mm weit, der Abstand zur Kamera 4300 mm.)
Wichtig ist dabei, die reflektierten Strahlen möglichst genau in Richtung des einfallenden Strahls zu lenken, weil eine Abweichung in der Richtung einen zusätzlichen Versatz erzeugt.
Wichtig ist dabei, die reflektierten Strahlen möglichst genau in Richtung des einfallenden Strahls zu lenken, weil eine Abweichung in der Richtung einen zusätzlichen Versatz erzeugt.
Reflexe (von einer zweiten Kamera) auf einem Schirm vor dem Laser, der durch das Loch in der Mitte strahlt.
Die Aufgabe besteht jetzt darin, den Sensor so zu verkippen, dass die beiden Hauptreflexe möglichst genau aufeinander fallen und zwar nachdem die Kamera so ausgerichtet wurde, dass der Glasreflex, der der hellste ist, durch das Loch zurück in den Laser fällt.
Damit ist das Wichtigste für die Astro-Anwendung, die Winkeljustage, leicht und ohne großen Aufwand zu schaffen. Der genaue Abstand des Sensors zum Teleskop oder Objektiv ist nur wichtig, wenn die Autofokusfunktion außerhalb des LiveView benötigt wird. Zwar wird auch für ein Korrekturelement (Komakorrektor) ein definierter Abstand benötigt, aber in der Regel reicht es dafür aus, die Sensorschrauben ausgehend von der Anschlagsposition um 360 Grad - abzüglich z.B. 0.3 Umdrehungen für die Korrektur eines ausgebauten LPF2 - herauszudrehen. Nach meiner Erfahrung stimmt sie dann auf +/- 0.1 mm genau.
Falls es doch einmal genauer sein muss, gibt es aber auch eine Möglichkeit, die Sensorposition optisch zu messen und entsprechend zu korrigieren:
Die Aufgabe besteht jetzt darin, den Sensor so zu verkippen, dass die beiden Hauptreflexe möglichst genau aufeinander fallen und zwar nachdem die Kamera so ausgerichtet wurde, dass der Glasreflex, der der hellste ist, durch das Loch zurück in den Laser fällt.
Damit ist das Wichtigste für die Astro-Anwendung, die Winkeljustage, leicht und ohne großen Aufwand zu schaffen. Der genaue Abstand des Sensors zum Teleskop oder Objektiv ist nur wichtig, wenn die Autofokusfunktion außerhalb des LiveView benötigt wird. Zwar wird auch für ein Korrekturelement (Komakorrektor) ein definierter Abstand benötigt, aber in der Regel reicht es dafür aus, die Sensorschrauben ausgehend von der Anschlagsposition um 360 Grad - abzüglich z.B. 0.3 Umdrehungen für die Korrektur eines ausgebauten LPF2 - herauszudrehen. Nach meiner Erfahrung stimmt sie dann auf +/- 0.1 mm genau.
Falls es doch einmal genauer sein muss, gibt es aber auch eine Möglichkeit, die Sensorposition optisch zu messen und entsprechend zu korrigieren:
Messung der Sensorposition
Für die genaue Einstellung der Sensorposition verwende ich ebenfalls die Reflexion am Sensor und zusätzlich den Beugungseffekt. Der Beugungseffekt entsteht dadurch, dass die Sensoroberfläche nicht perfekt gleichförmig ist, sondern ein regelmäßiges Pixel-Muster aufweist, an dem Licht gebeugt wird. Man sieht das sehr schön an den schillernden Farben, die ein Sensor bei Lichteinfall zeigt. Diese Farben haben nichts mit der RGB-Matrix zu tun, sondern sind auch auch bei Monochrom-Sensoren zu beobachten.
Ein einfarbiger, paralleler Lichtstrahl wird durch diesen Effekt in ganz bestimmte, zusätzliche Richtungen reflektiert, die man aus der Sensorstruktur berechnen kann.
Tatsächlich erkennt man auf dem zweiten Reflex-Bild oben in den Ecken des Schirms zusätzliche, schwache Lichtpunkte. Wenn man deren Lage sorgfältig vermisst und den Abstand des Schirms zum Bajonett kennt, kann man damit den Abstand des Sensors zum Bajonett berechnen.
Für die genaue Einstellung der Sensorposition verwende ich ebenfalls die Reflexion am Sensor und zusätzlich den Beugungseffekt. Der Beugungseffekt entsteht dadurch, dass die Sensoroberfläche nicht perfekt gleichförmig ist, sondern ein regelmäßiges Pixel-Muster aufweist, an dem Licht gebeugt wird. Man sieht das sehr schön an den schillernden Farben, die ein Sensor bei Lichteinfall zeigt. Diese Farben haben nichts mit der RGB-Matrix zu tun, sondern sind auch auch bei Monochrom-Sensoren zu beobachten.
Ein einfarbiger, paralleler Lichtstrahl wird durch diesen Effekt in ganz bestimmte, zusätzliche Richtungen reflektiert, die man aus der Sensorstruktur berechnen kann.
Tatsächlich erkennt man auf dem zweiten Reflex-Bild oben in den Ecken des Schirms zusätzliche, schwache Lichtpunkte. Wenn man deren Lage sorgfältig vermisst und den Abstand des Schirms zum Bajonett kennt, kann man damit den Abstand des Sensors zum Bajonett berechnen.
Hier sieht man diese Beugungsreflexe auf einem speziellen Schirm, der den großen Vorteil hat, dass sein Abstand zum Bajonett genau bekannt, nämlich gleich 0, ist. Die Lage der Reflexe hängt dann direkt vom Abstand zwischen Sensor und Bajonett ab. Für den Schirm ist Millimeterpapier kameraseitig mit Klarlack auf ein (Objektträger-) Gläschen geklebt, so dass es leicht durchscheinend wird und direkt und plan auf dem Bajonett aufliegt. Durch das Loch in der Mitte trifft der Laserstrahl auf den Sensor und der zentrale Reflex tritt dort wieder aus und trifft wieder den Laser. Wichtig ist dabei, dass dieser Hauptreflex möglichst genau wieder in den Laser zurückfällt. Dann trifft der Laserstrahl senkrecht auf den Sensor und die Formel zur Berechnung der Sensorposition (s.u.) wird besonders einfach:
d = x · sqrt(1-y²) / y, mit: y = m · lambda / a
Dabei ist
d: (optischer) Abstand Sensor – Bajonettx: Abstand eines Reflexes auf dem Schirm zum Zentrumm: Ordnung des Reflexes (1, 2, 3, …)lambda: Wellenlänge des Lasers, 532 nm für grüne Laserpointera: Gitterkonstante
Die Gitterkonstante a ist die Größe der Strukturen, an denen das Licht gebeugt wird. Im Fall eines RGB-Sensors ist es die Größe einer RG/GB Gruppe, also die doppelte Pixelgröße.
Erfreulicherweise erhält man den so berechneten Abstand des Sensors zum Bajonett gleich als optischen Abstand, also den durch die Gläser im Lichtweg gegenüber dem mechanischen Abstand verringerten Wert, den man für die Einstellung braucht. Das bedeutet, wenn man vor einem Filterausbau einen Abstand von 44 mm gemessen hat, stellt man den Abstand danach auch wieder auf 44 mm ein.
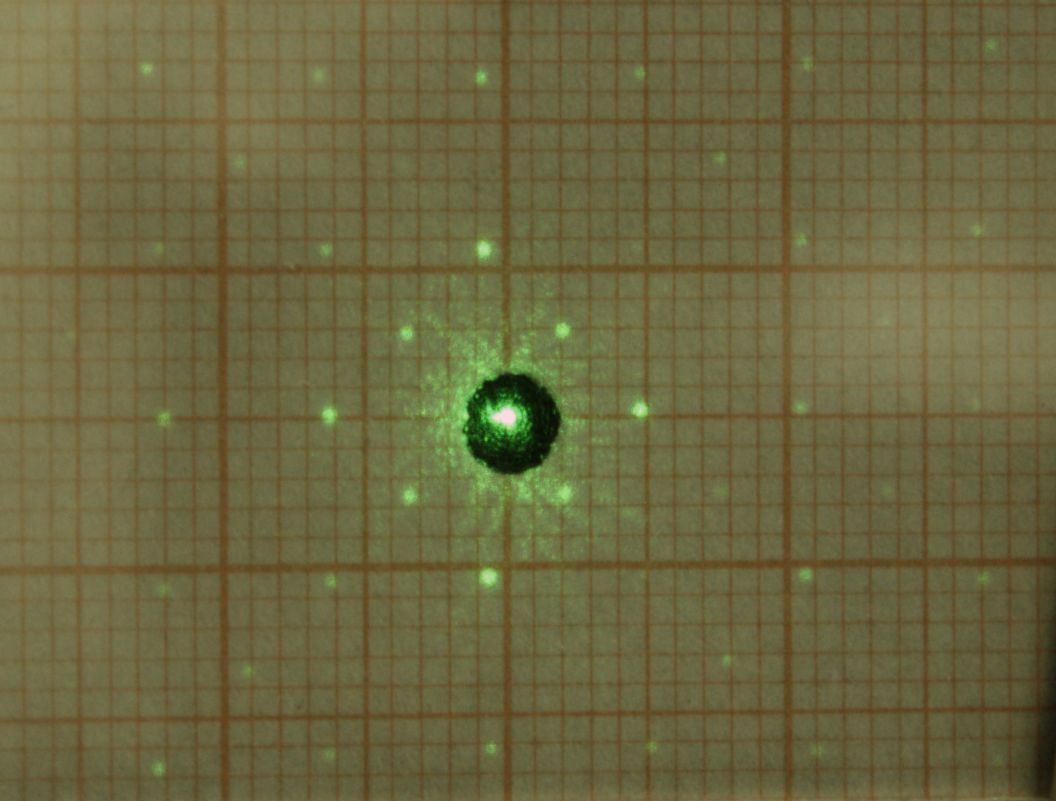
Hier ist das Beugungsbild vergrößert dargestellt. Man sieht, dass die Reflexe auf einem quadratischen Raster mit einer Weite von etwa 2.8 mm liegen. Die innersten 4 Punkte gehören zur Ordnung 1, von der nur die diagonalen Elemente zu erkennen sind. Von der zweiten Ordnung (mit einem Zentrumsabstand von ca. 5.6 mm je Richtung) sind dafür die diagonalen Elemente schwächer als die senkrecht und waagrecht liegenden, die in einer Richtung von nullter Ordnung sind. Diese Helligkeitsverteilung hängt stark vom Durchmesser des Laserstrahls ab bzw. davon, wie viele Pixel vom Laser beleuchtet werden.
Wenn man die 4. Ordnung (bei 11.2 mm) betrachtet, fällt eine Art Kissenverzerrung auf. Das bedeutet, dass die Kriterien für die Fraunhofer-Beugung nicht ausreichend erfüllt sind. Man kann deshalb für weit außen liegende Reflexe die Gleichung von oben nicht mehr anwenden. Für die Punkte der Ordnung (4,0) auf der Waagrechten und (0,4) auf der Senkrechten durch das Zentrum habe ich aber immer Ergebnisse bekommen, die so gut waren wie die Ablesegenauigkeit von etwa 0.1 mm.
Als Beispiel hier die Rechnung für die Ordnung (4,0):
2 · x = 22.4 mm (Abstand der 4. Ordnung links und rechts des Zentrums)
Die Kamera ist eine EOS 60D mit einer Pixelgröße von ca. 4.30 µm, also a = 8.6 µm.
Damit wird dann
y = 4 · 532 nm / 8.6 µm = 0.2474 mit sqrt(1-y²) / y = 3.916 .
Der Abstand des Sensors vom Schirm wird damit:
d = x · sqrt(1-y²) / y = 11.2 mm · 3.916 = 43.86 mm
Die Abweichung vom Canon EF Auflagemaß beträgt damit 0.14 mm, ist also ungefähr so groß wie die (relative) Unsicherheit bei der Ablesung von '2·x'.
Eine gewisse Unsicherheit bei der Berechnung ist die Pixelgröße, die man für die Kameras findet. Ich habe für die 60D statt den 4.3 µm auch schon 4.29 µm gefunden, was auch etwa 0.1 mm Unterschied am Ergebnis ausmacht, und 'offizielle', exakte Werte konnte ich leider nicht auftreiben.
Eine weitere potenzielle Fehlerquelle ist das Millimeterpapier, das beim Aufkleben evtl. noch seine Größe leicht ändern könnte. Zur Verbesserung der Genauigkeit ist es deshalb keine schlechte Idee, die Messung einmal durchzuführen, bevor man die Kamera zerlegt um damit die Methode zu kalibrieren.
Direkte Messung mithilfe des Sensors
Zur Verbesserung der Ablesegenauigkeit ist mir noch eine Variante eingefallen, die allerdings nur mit einer funktionsbereiten Kamera anwendbar ist. Und zwar legt man statt des Millimeterpapiers einen Oberflächenspiegel (mit einem Loch in der Mitte) auf das Bajonett auf. Dann werden die Beugungsreflexe auf den Sensor zurückgeworfen, den man mit sehr hoher Auflösung auslesen kann. Außerdem verdoppelt sich dabei der Abstand der Reflexe, so dass man leicht die erste oder zweite Ordnung verwenden kann, die von der Kissenverzerrung praktisch nicht betroffen ist.
Die Abstandsberechnung ist dabei fast identisch, man muss nur zusätzlich noch den Abstand von Pixeln in Millimeter umrechnen und dann durch zwei teilen, weil der Weg, den der Reflex zurücklegt, ja doppelt so lang ist.
Und das Beste ist: Man braucht gar keinen speziellen Spiegel dazu – auch ein Glas reflektiert ausreichend gut für diesen Zweck.
So sieht der Lichtweg aus, wenn das Glas verspiegelt ist.
Wenn man ein unbeschichtetes Glas als Spiegel verwendet, treten die gebeugten Strahlen großteils wieder aus, nur 4% ihrer Intensität wird reflektiert. Vom austretenden Strahlanteil bekommt man eine zusätzliche Reflexion an der Glasaußenseite und auf dem Sensor erscheinen dann doppelte Punkte:
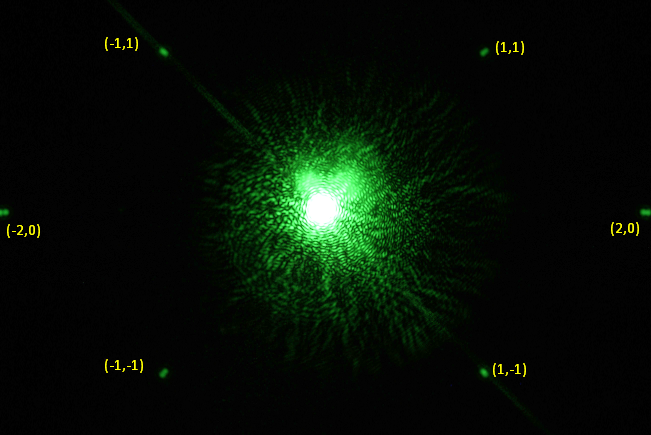
Obwohl die Belichtungszeit für diese Aufnahme nur 1/250 s betrug, ist der Sensor um den direkten Laserpunkt massiv überbelichtet, was sich aber nicht vermeiden lässt, wenn man die Beugungsreflexe noch erkennen will. Stört aber auch nicht weiter, und die geringe Laserleistung kann dem Sensor auch nicht schaden.
Die Reflexe zweiter Ordnung passten hier gerade noch auf den APSC Sensor, und es ist gut zu erkennen, dass die Beugungsreflexe immer aus zwei Punkten bestehen, wobei die äußeren von der äußeren Glasseite stammen.
Zur Berechnung der Sensorposition nimmt man dann am besten die Abstände der inneren Punkte zu ihren Gegenübern, dann ist es egal, wie dick das Glas ist.
Der Abstand w zwischen dem (-1,-1) und dem (1,-1) Reflex war hier 2540 Pixel, die wieder eine Größe von ca. 4.3 µm haben. Eingesetzt ergibt das dann (mit dem y für die erste Ordnung)
d = w/4 · sqrt(1-y1²) / y1 = 2540/4 · 4.3 µm · 16.13 = 44.06 mm
Mit den (-2,0) und (2,0) Reflexen ergibt sich d = 44.01 mm.
Die Begrenzung der Genauigkeit kommt hier einmal von den Durchmessern der Reflexpunkte und evtl. einem Fehler in der eingesetzten Pixelgröße. Und irgendwann werden auch noch die Nachkommastellen der Laserwellenlänge relevant.
Laser
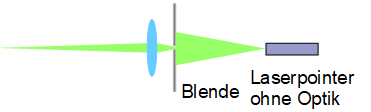
Um die Qualität des Laserstrahls zu verbessern, habe ich ihn erst noch aufgeweitet, dann mit einer kleinen Blende den größten Teil ausgeblendet und anschließend so fokussiert, dass der Fokus in der Nähe des Sensors liegt. Das hat neben der besseren Abbildung noch den Vorteil, dass ich die Leistung dadurch auf weniger als ein Hundertstel reduziert habe, was einen Laserpointer dann wirklich ungefährlich macht. Zum Aufweiten kann man einfach die eingebaute Linse entfernen. Zum Fokussieren braucht man eine Brennweite, die etwas größer als die Hälfte des gewünschten Abstands der Linse zum Laser oder zum Sensor ist, z.B. f = 100 mm.
Bei preiswerten grünen Lasern handelt es sich um frequenzverdoppelte Nd:YAG Laser. Die haben gegenüber Diodenlasern den Vorteil, dass die Wellenlänge (532 nm) genau bekannt ist und die Strahlqualität konstruktionsbedingt nicht zu schlecht sein darf. Rote Laser sind Diodenlaser, die es in verschiedenen Wellenlängen gibt. Man muss also zuerst mal herausfinden, ob es z.B. 635 nm oder etwa 650 nm sind. Sie haben den zusätzlichen Nachteil, dass sie vom LPF2 Filter stark geschwächt werden, so dass Reflexe vom Sensor unmodifizierter Kameras recht dunkel ausfallen.
Zum Schluss noch die Gittergleichung für die Berechnung des Beugungsmusters:
Der Winkel phi des Hauptmaximums mit der Ordnung m eines Beugungsgitters liegt bei
sin(phi) = sin(phi0) ± m · lambda/a
wobei der Einfallswinkel phi0 am besten auf 0° eingestellt wird.
Seine Position x auf einem Schirm im Abstand d ist
x = d · tan(phi)
Beides zusammen gibt
d = x / tan(asin(y)) mit: y = m · lambda/a
oder auch
d = x · sqrt(1-y²) / y
Zuletzt aktualisiert am 26.09.2024